Логика – наука, изучающая законы и формы мышления, изучает абстрактное мышление как средство познания объективного мира.
Этапы развития логики:
I этап – формальная логика. Основатель – Аристотель (384-322 гг. до н.э.), ввел основные формы абстрактного мышления.
II этап – математическая логика. Основатель –немецкий ученый и философ Лейбниц (1642-1716), предпринял попытку логических вычислений.
III этап – математическая логика (булева алгебра). Основатель – английский математик Джордж Буль (1815-1864), ввел алфавит, орфографию и грамматику для математической логики.
Высказывание (суждение) – это форма мышления, выраженная с помощью понятий, посредством которой что-либо утверждают или отрицают о предметах, их свойствах и отношениях между ними.
Высказывания бывают простые и сложные.
Простое высказывание (логическая переменная) содержит только одну простую мысль.
Сложное высказывание (логическая функция) содержит несколько простых мыслей, соединенных между собой с помощью логических операций (и, или, частицей не).
Доказательство есть мыслительный процесс, направленный на подтверждение или опровержение какого-либо положения посредством других несомненных, ранее обоснованных доводов.
Алгебра логики это математический аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают логические высказывания.
Объектами алгебры логики являются высказывания.
Значение логической функции можно определить с помощью специальной таблицы (таблицы истинности) и графически проиллюстрировать с помощью диаграмм Эйлера-Венна.
Таблица истинности - таблица, в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.
A и B
– логические
переменные, n=2, F логическая функция.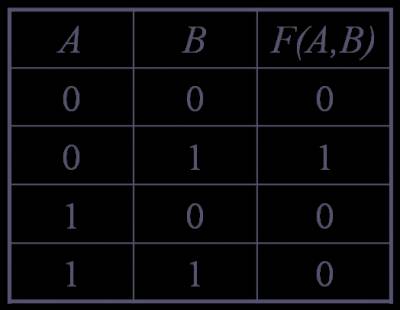
Отрицание – это
логическая операция, которая каждому простому высказыванию ставит в
соответствие составное высказывание, заключающееся в том, что исходное
высказывание отрицается.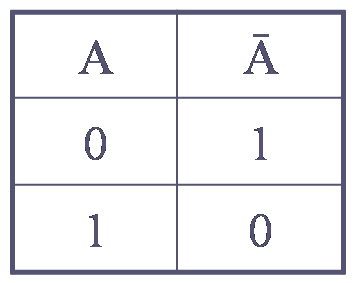
Конъюнкция
– это
логическая операция, ставящая в соответствие каждым двум простым высказываниям
составное высказывание, являющееся истинным тогда и только тогда, когда оба
исходных высказывания истинны.
Дизъюнкция
– это
логическая операция, которая каждым двум простым высказываниям ставит в
соответствие составное высказывание, являющееся ложным тогда и только тогда,
когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух
образующих его высказываний истинно.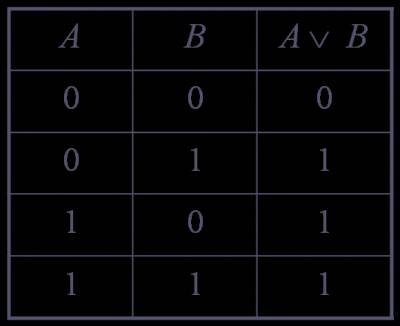
ПОРЯДОК ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
1) операция в
скобках;
2) отрицание;
3) логическое умножение;
4) логическое сложение;
5) импликация;
6) эквиваленция.
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫ ИСТИННОСТИ
Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице, которое равно m=2n;
3. подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице;
4. ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
5. заполнить столбцы входных переменных наборами значений;
6. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.